Momentum Cases
The approach you can take to answering a question about momentum changes in a two object collision depends on how you define the system.
Consider both approaches below, and copy one or both sets of notes into your notebook.
Approach 1 (one-object system)
If you define the system as including only one object (object A), then your initial momentum for the system will be only the momentum of that object: $(m_A \cdot \Delta v_A)$.
\[p = m_A \times \Delta V_A\] \[\mathrm{momentum} = \mathrm{mass} \times \text{change in velocity}\]Any gain in momentum of the system must come from an object outside of the system exerting a force, which must lose exactly the amount of momentum gained by the system. Thus you will model such a system mathematically by determining the gain (or loss) in momentum of the single-object system and setting that equal to the loss (or gain) in momentum of the object outside of the system $-(m_B \cdot \Delta v_B)$.
Therefore, defining the system this way, you will have the equation:
\[m_A \cdot \Delta v_A = -m_B \cdot \Delta v_B\]The second object (object B) has lost momentum in this example, so its momentum term will be negative. Remember that the change in velocity of one of the objects may also be in the negative direction!
where $\Delta v_A$ is the change in velocity of object A and $\Delta v_B$ is the change in velocity of object B.
Approach 2 (two-object system)
If you define the system as including both objects involved in the collision, then your initial momentum for the system (before the collision) will be the sum of the initial momenta of both objects
\[(m_A \cdot v_A + m_B \cdot v_B)\]Because there is no external force acting on the system in the system that is bounded this way, the total momentum of the system after the collision should not change, in other words, the change of momentum will be 0.
\[p = p'\] \[\text{total momentum before} = \text{total momentum after}\]Thus you will model such a system mathematically by setting the initial momentum equal to the final momentum producing the equation:
\[m_A \cdot v_A + m_B \cdot v_B = m_A \cdot v'_A + m_B \cdot v'_B\]where $v_A$ and $v_B$ are the initial velocities of objects A and B, and $v’_A$ and $v’_B$ are the final velocities of objects A and B after the collision.
Note: You might notice that these approaches are actually doing the same math, but in a different way. Which is exactly the same model that we use in the two-object system approach!
Worked Examples
Example 1: Separate Objects After Collision
A 5 kg bowling ball rolling at 8 m/s collides with a stationary 2 kg pin. After the collision, the bowling ball continues moving forward at 6 m/s.
Find: The final velocity of the pin.
Approach 2
\(m_A \cdot v_A + m_B \cdot v_B = m_A \cdot v'_A + m_B \cdot v'_B\)
Given:
$m_A = 5 \text{ kg}$
$v_A = 8 \text{ m/s}$
$v’_A = 6 \text{ m/s}$
$m_B = 2 \text{ kg}$
$v_B = 0 \text{ m/s}$
$v’_B = ?$
Step 1: Solve for $v’_B$
Step 2: Substitute values
\(\begin{align} v'_B &= \frac{(5\text{ kg})(8\text{ m/s}) + (2\text{ kg})(0\text{ m/s}) - (5\text{ kg})(6\text{ m/s})}{2\text{ kg}}\\ v'_B &= \frac{40\text{ kg⋅m/s} + 0\text{ kg⋅m/s} - 30\text{ kg⋅m/s}}{2\text{ kg}}\\ v'_B &= \frac{10\text{ kg⋅m/s}}{2\text{ kg}} = 5.0\text{ m/s} \end{align}\)
Example 2: Objects Stick Together (Perfectly Inelastic)
A 1200 kg car traveling at 20 m/s rear-ends a stationary 1500 kg truck. After the collision, both vehicles move together as one unit.
Find: The velocity of both vehicles after they stick together.
Approach 2
\(m_A \cdot v_A + m_B \cdot v_B = (m_A + m_B) \cdot v'_{combined}\)
Given:
$m_A = 1200 \text{ kg}$
$v_A = 20 \text{ m/s}$
$m_B = 1500 \text{ kg}$
$v_B = 0 \text{ m/s}$
$v’_{combined} = ?$
Step 1: Solve for $v’_{combined}$
Step 2: Substitute values
Question 1
These data describe the outcome of a collision between two grocery carts, one empty (B) and one with groceries in it (A).
| Grocery cart | Mass | Initial velocity (v) | Final velocity (v’) |
|---|---|---|---|
| A | 60 kg | 0.50 m/s | 0.25 m/s |
| B | ? | 0 m/s | 0.75 m/s |
-
1a). Is this collision elastic, or inelastic? How do you know?
-
1b). What does our mathematical model predict the mass of grocery cart B must be?
-
1c). How many times larger was the magnitude of the change in velocity for cart B compared to cart A?
Question 2
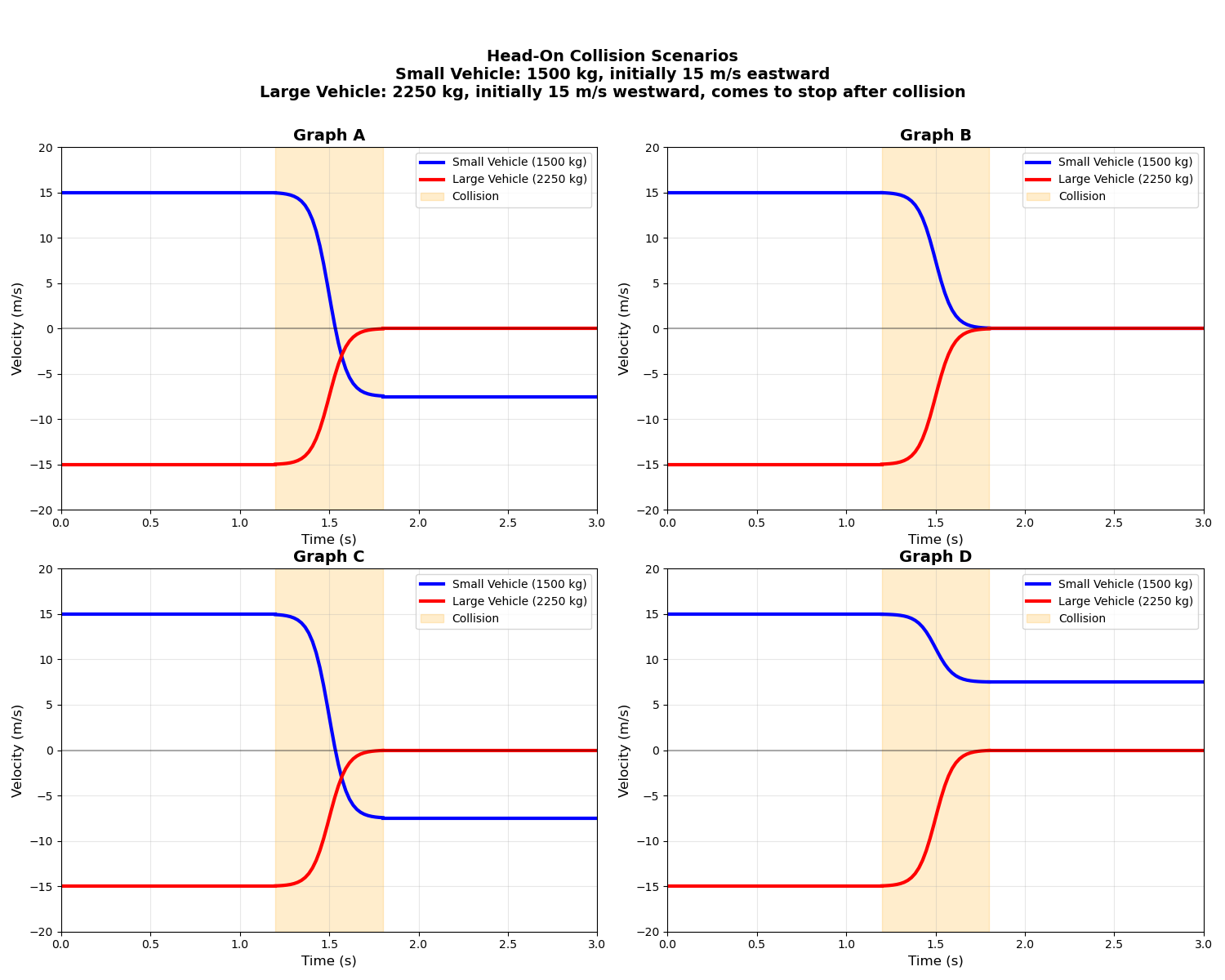
A head-on collision occurs between two vehicles. The smaller vehicle is 1500 kg and is moving at 15 m/s initially. The larger car is 2250 kg and is moving at 20 m/s in the opposite direction initially. The larger car comes to a stop as a result of the contact forces in the collision.
- 2.) For each graph, indicate whether it shows the expected velocity change in the smaller vehicle? (indicate yes or no for each, and explain why). Sketch the correct graph in your notebook.
Question 3
Switcher engines help move train cars around on tracks in train yards. To save time and fuel in this process, they sometimes uncouple a car they have been pushing, so it coasts along the track until it collides with a chain of stationary cars it needs to be connected to.


When this happens the couplers on the end of the train cars automatically catch, and a longer chain of cars is formed. The collision sometimes results in the entire longer chain of cars moving forward in the direction of the push.
3a). Is this collision elastic, or inelastic? How do you know?
3b). How fast must a tanker car have been moving before such a collision if the following is true?
- The tanker car collides with and couples to 11 other tanker cars
- You can assume that all 11 tanker cars together form a single object with mass $(11 \times m_{\text{tanker car}})$
- The entire set of 12 cars ends up moving together at 0.2 m/s as a result of this collision
- Every tanker car has a mass of 119,000 kg
Student Key
Question 1:
- 1a) Inelastic collision (objects do not separate completely)
- 1b) Mass of cart B = 20 kg
- 1c) Cart B’s velocity change is 3 times larger than cart A’s
Question 2:
- 2a) No (shows wrong direction of velocity change)
- 2b) Yes (shows correct velocity change from +15 m/s to -5 m/s)
- 2c) No (shows wrong final velocity)
- 2d) No (shows wrong velocity change pattern)
Question 3:
- 3a) Inelastic collision (cars couple together)
- 3b) Initial velocity = 2.4 m/s