P3L5 Collision Simulation Lab Guide
Introduction
This simulation lab allows you to investigate how objects of different masses interact during collisions. Using a virtual environment, you’ll test whether the mathematical relationship between mass ratios and velocity changes holds true across various collision scenarios. The simulation provides precise control over mass, velocity, and collision type (elastic or inelastic), enabling you to collect accurate data without the friction and measurement limitations of physical experiments. By systematically changing variables and observing outcomes, you’ll determine if the momentum principles we’ve studied apply universally to all collisions.
Background: What We’re Testing
In our previous lesson, we discovered this mathematical relationship:
\[\frac{m_A}{m_B} = -\frac{\Delta v_B}{\Delta v_A}\]Today’s Question: Does this relationship work for ALL types of collisions, or just the specific ones we tested before?
Part 1: Getting Started with the Simulation
Step 1: Familiarize Yourself with the Controls
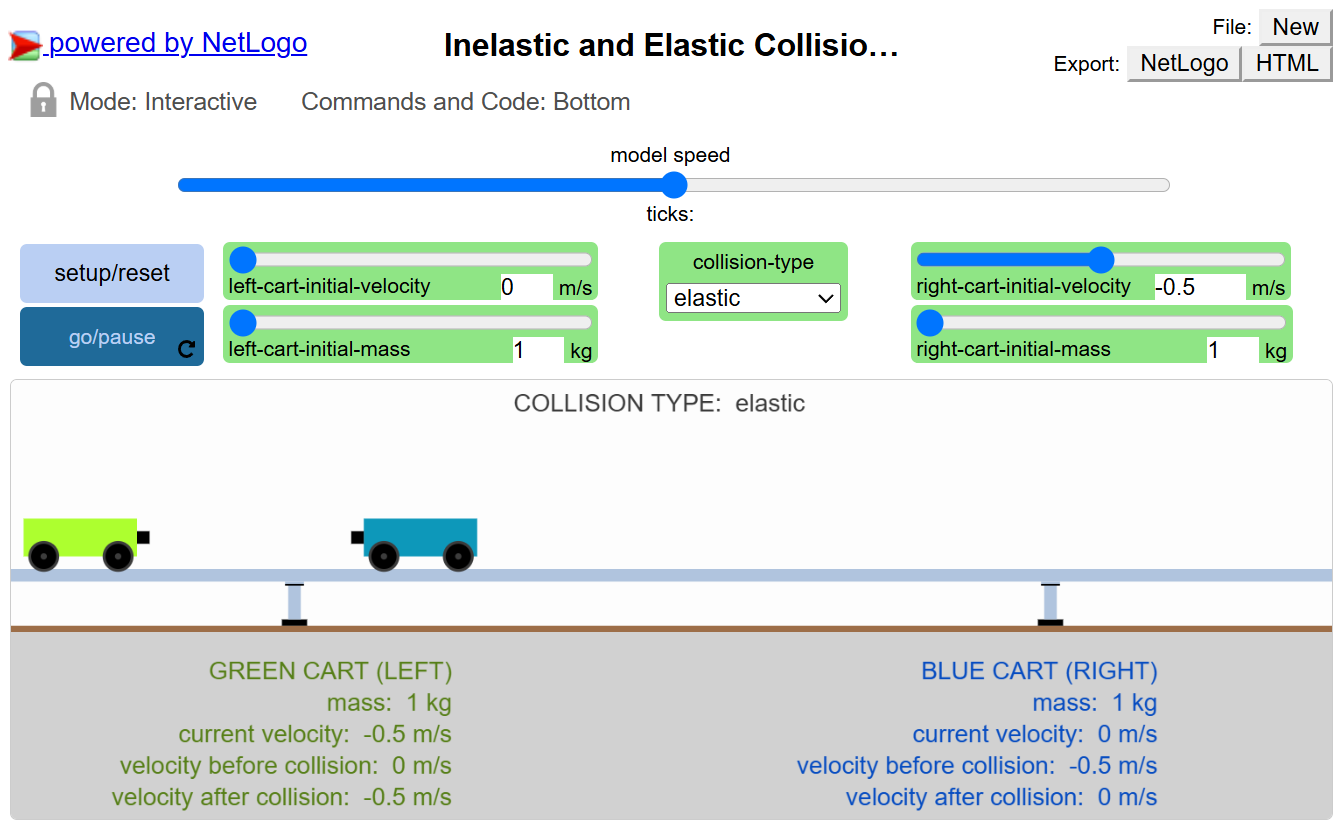
Mass Sliders:
- Adjust the mass of each cart (Cart A and Cart B)
- Range: typically 1-10 kg
Velocity Sliders:
- Set the initial velocity of each cart
- Positive values = moving right
- Negative values = moving left
- Zero = stationary
Collision Type Selector:
- Elastic: Carts bounce apart (like billiard balls)
- Inelastic: Carts stick together after collision
Control Buttons:
- SETUP/RESET: Apply your chosen settings
- GO/PAUSE: Run the simulation
Step 3: Practice Run
Before collecting data, try one practice run:
- Set Cart A: mass = 2 kg, velocity = 1 m/s
- Set Cart B: mass = 1 kg, velocity = 0 m/s
- Choose “Elastic” collision
- Click SETUP/RESET, then GO
- Observe what happens!
Part 2: Data Collection
Your Objective
Test our mathematical relationship systematically with at least 6 different collision scenarios that follow proper experimental design:
Required Test Categories:
- Control Group: Repeat one scenario from our previous lesson to verify consistency
- Variable: Collision Type - Test both elastic and inelastic with identical starting conditions
- Variable: Mass Ratio - Test different mass ratios (1:1, 1:2, 1:3, 2:3, etc.)
- Variable: Initial Velocities - Test scenarios where both objects are moving initially
- Variable: Velocity Magnitude - Test high-speed vs. low-speed collisions with same mass ratio
Scientific Method Requirements
Before You Begin:
- Hypothesis: Write a prediction about whether the mathematical relationship will hold for all scenarios
- Independent Variables: What you will systematically change (mass, velocity, collision type)
- Dependent Variables: What you will measure (final velocities, Δv values)
- Controls: What you will keep constant between related tests
Data Collection Table
For each collision, record the following data in a table like the one below. Make sure to fill in all columns for each trial.
| Trial | Collision Type | Mass A (kg) |
Mass B (kg) |
Initial $v_A$ (m/s) |
Initial $v_B$ (m/s) |
Final $v_A’$ (m/s) |
Final $v_B’$ (m/s) |
Purpose/Variable Tested |
|---|---|---|---|---|---|---|---|---|
| 1 | Control (repeat previous) | |||||||
| 2 | Test collision type | |||||||
| 3 | Test mass ratio | |||||||
| 4 | Test both moving | |||||||
| 5 | Test velocity magnitude | |||||||
| 6 | [Your choice] |
Experimental Design Guidelines
For Valid Comparisons:
- Change ONE variable at a time between related trials
- Keep all other variables constant when testing a specific relationship
- Use consistent units throughout all measurements
- Record exact values - avoid rounding during data collection
- Plan your trials before starting to ensure systematic testing
Example of Proper Variable Control:
- Trials 2 & 3: Same masses and velocities, only change elastic → inelastic
- Trials 4 & 5: Same collision type and masses, only change velocity magnitudes
- Trials 5 & 6: Same collision type and velocities, only change mass ratio
Tips for Scientific Data Collection
- Write down your plan first - which variable will you test in each trial?
- Use simple, round numbers when possible (makes calculations easier)
- Test extremes - try very different mass ratios (like 10:1) or velocity differences
- Repeat suspicious results - if something doesn’t work, try the same conditions again
- Document observations - note anything unusual you observe
Part 3: Testing Our Mathematical Model
For Each Trial, Calculate:
Step 1: Find the change in velocity (Δv) for each cart
- $\Delta v_A = v_A’ - v_A$ (Final velocity - Initial velocity)
- $\Delta v_B = v_B’ - v_B$ (Final velocity - Initial velocity)
Step 2: Calculate the ratio of velocity changes
- Velocity change ratio = $\frac{\Delta v_B}{\Delta v_A}$
Step 3: Test our relationship
- Does: $\frac{m_A}{m_B} = -\frac{\Delta v_B}{\Delta v_A}$ ?
- (Note the negative sign!)
Sample Calculation
If Cart A (2 kg) goes from 3 m/s to 1 m/s, and Cart B (1 kg) goes from 0 m/s to 4 m/s:
- $\Delta v_A = 1 - 3 = -2$ m/s
- $\Delta v_B = 4 - 0 = +4$ m/s
- Mass ratio: $\frac{m_A}{m_B} = \frac{2}{1} = 2$
- Velocity change ratio: $\frac{\Delta v_B}{\Delta v_A} = \frac{4}{-2} = -2$
Test: Does $2 = -(-2)$? YES! ✓
Calculation Template
For each trial, complete these calculations:
Trial #_____ Calculations
Initial Conditions:
- Cart A: mass = ___ kg, velocity = ___ m/s
- Cart B: mass = ___ kg, velocity = ___ m/s
Final Velocities:
- Cart A final velocity = _____ m/s
- Cart B final velocity = _____ m/s
Velocity Changes:
- $\Delta v_A = v_A’ - v_A = $ _____ m/s
- $\Delta v_B = v_B’ - v_B = $ _____ m/s
Ratios:
- Mass ratio: $\frac{m_A}{m_B} = $ _____
- Velocity change ratio: $-\frac{\Delta v_B}{\Delta v_A} = $ _____
Testing the Relationship:
- Does $\frac{m_A}{m_B} = -\frac{\Delta v_B}{\Delta v_A}$ ?
Percent Error (optional):
$\text{Error} = \frac{\text{experimental - theoretical}}{\text{theoretical}} \times 100\% = $ _____%