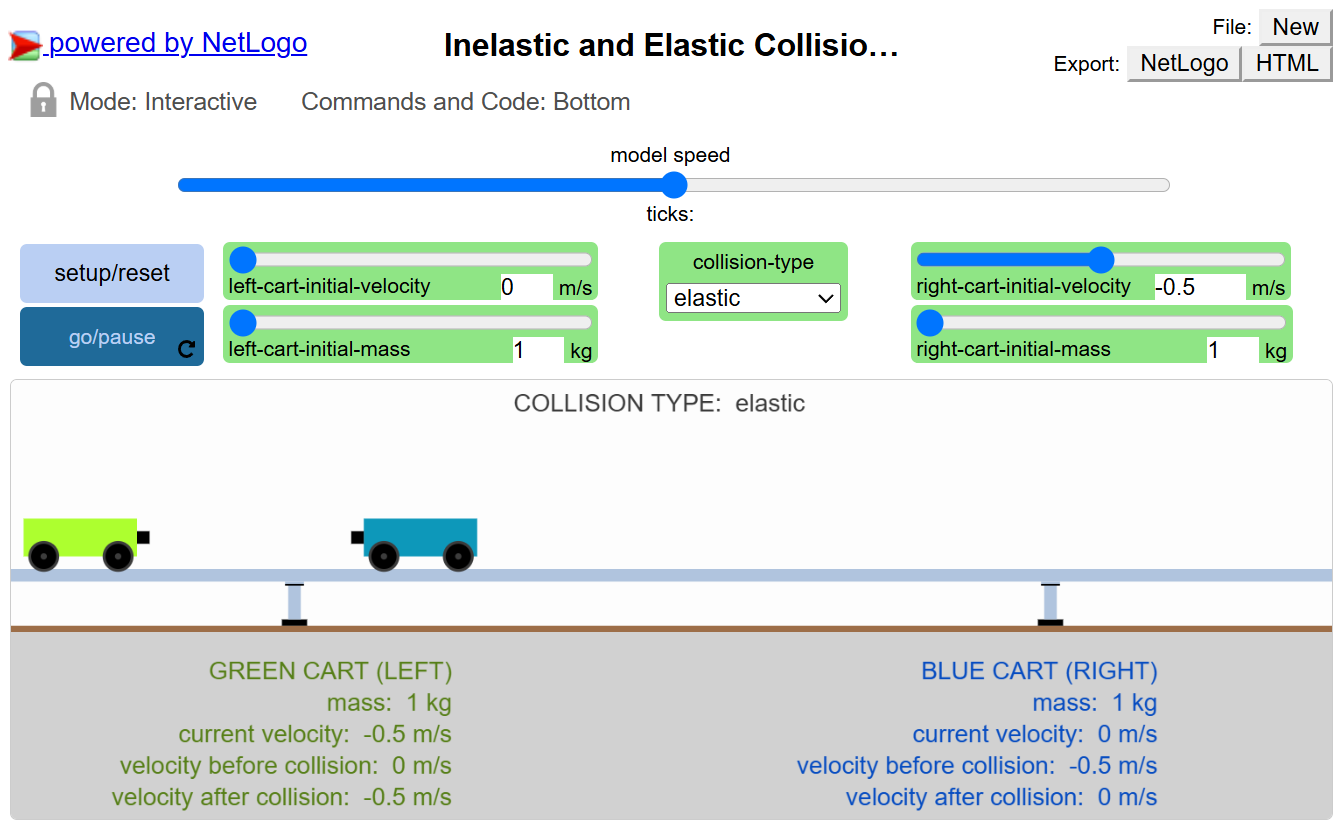
P3L5: Mass, Speed, and Force

Is there a similar mathematical relationship between the masses and the changes in velocity for two objects in any other collision conditions?

In our previous investigations, we explored how the masses of two colliding objects relate to their changes in velocity. We found a mathematical relationship that when one object was initially at rest, the ratio of masses equals the negative ratio of velocity changes:

\[\frac{m_A}{m_B} = -\frac{\Delta v_B}{\Delta v_A}\]

This relationship helped us make predictions about collisions with specific conditions, but we haven’t tested whether it works in all situations. Today, we’ll investigate if this same relationship applies when both objects are initially moving, or when objects bounce apart instead of sticking together. By testing our model under different conditions, we can determine if we’ve discovered a more general principle that might help explain all collisions.

---

Part I: Testing Our Mathematical Model

Investigation Question

In our previous lesson, we discovered a mathematical relationship between mass and velocity changes in collisions:

\[\frac{m_A}{m_B} = -\frac{\Delta v_B}{\Delta v_A}\]

But does this relationship hold for different collision conditions beyond what we’ve tested?

Testing with Simulation

We’ll use a collision simulation to test our mathematical model systematically under various conditions:

• Different mass ratios
• Different initial velocities
• Both elastic and inelastic collisions

Lab Activity: Complete the P3L5 Collision Simulation Lab to systematically test our mathematical relationship. The lab guide provides step-by-step instructions for:

• Setting up different collision scenarios
• Collecting accurate data using proper experimental design
• Testing the mathematical relationship
• Analyzing your results

Follow the lab guide to conduct your investigation, then return here to learn about the deeper meaning of your discoveries.

---

Part II: Discovering Conservation

Simplifying Our Equation

When we cross-multiply our ratio equation, something important emerges:

\[\begin{align} \frac{m_A}{m_B} &= -\frac{\Delta v_B}{\Delta v_A} \\ \\ \text{Cross-multiplying:} \\ m_A \times \Delta v_A &= -m_B \times \Delta v_B \\ \\ \text{Rearranging:} \\ m_A \Delta v_A + m_B \Delta v_B &= 0 \end{align}\]

This important equation shows us that the sum of mass times velocity change equals zero in any collision.

The Conserved Quantity

The equation tells us that the quantity $m \times \Delta v$ appears to be conserved in collisions - what one object loses, the other gains exactly.

This means that in any collision:

• The total amount of $m \times \Delta v$ in the system remains constant
• When one object’s $m \times \Delta v$ increases, the other’s decreases by the same amount
• The overall change in the system is zero

---

Part III: Visualizing with Geometry

Rectangle Model

We can visualize the conserved quantity using rectangles where:

• Width = mass (kg)
• Height = change in velocity (m/s)
• Area = mass × change in velocity

Example: 2 kg and 4 kg Cart Collision

Let’s examine a collision where:

• Cart A: 2 kg, experiences a velocity change of +6 m/s
• Cart B: 4 kg, experiences a velocity change of -3 m/s

We can verify that momentum is conserved by calculating the change in momentum for each cart:

• Cart A momentum change: $m_A \times \Delta v_A = 2 \text{ kg} \times 6 \text{ m/s} = +12 \text{ kg}\cdot\text{m/s}$
• Cart B momentum change: $m_B \times \Delta v_B = 4 \text{ kg} \times (-3 \text{ m/s}) = -12 \text{ kg}\cdot\text{m/s}$
• Total momentum change: $+12 \text{ kg}\cdot\text{m/s} + (-12 \text{ kg}\cdot\text{m/s}) = 0 \text{ kg}\cdot\text{m/s}$

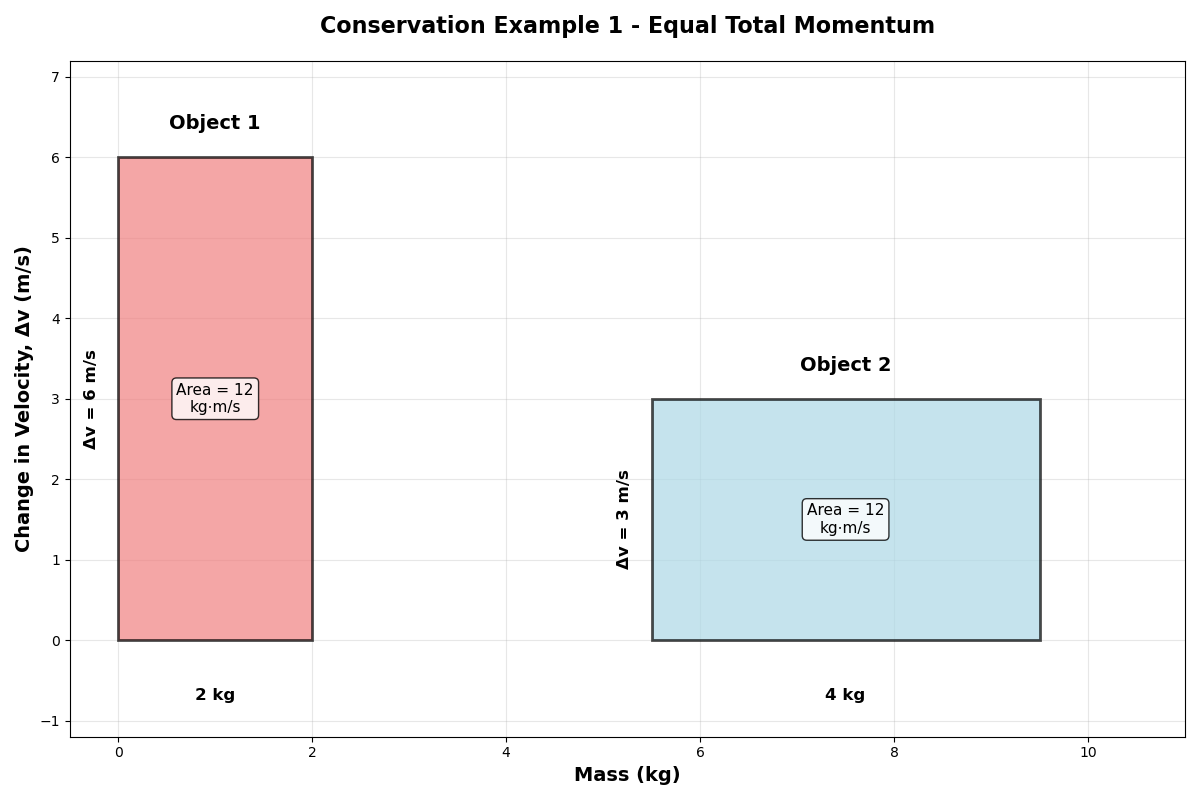
Rectangle representation for momentum changes:

• First cart (2 kg):
  • Width = 2 kg
  • Height = Δv = +6 m/s
  • Area = $2 \text{ kg} \times 6 \text{ m/s} = +12 \text{ kg}\cdot\text{m/s}$
• Second cart (4 kg):
  • Width = 4 kg
  • Height = Δv = -3 m/s
  • Area = $4 \text{ kg} \times (-3 \text{ m/s}) = -12 \text{ kg}\cdot\text{m/s}$

Notice that the total momentum change is zero: +12 kg⋅m/s + (-12 kg⋅m/s) = 0, confirming conservation of momentum. The increase in momentum of the lighter cart exactly equals the decrease in momentum of the heavier cart.

---

Part IV: Understanding Momentum

Key Definitions and Vocabulary

Defining Momentum

The conserved quantity we discovered has a name: momentum

• Momentum = mass × velocity (p = mv)
• Change in momentum = mass × change in velocity (Δp = mΔv)

Conservation of Momentum

Our equation can be rewritten to show momentum conservation:

Before collision: $p_A + p_B = m_A v_A + m_B v_B$

After collision: $p_A’ + p_B’ = m_A v_A’ + m_B v_B’$

Conservation principle: $p_A + p_B = p_A’ + p_B’$

This tells us that the total momentum before a collision equals the total momentum after the collision.

Types of Collisions

Elastic collision: Objects bounce apart after collision

• Examples: billiard balls, bouncing superballs
• Objects separate after impact
• Both momentum and kinetic energy are conserved
• Objects have different final velocities

Inelastic collision: Objects stick together or deform during collision

• Examples: car crashes, putty balls hitting a wall
• Objects may stick together or remain in contact
• Momentum is conserved, but kinetic energy is not
• Perfectly inelastic: Objects stick together completely after collision

Understanding Perfectly Inelastic Collisions

In perfectly inelastic collisions, objects stick together after impact, forming a single combined object moving with the same final velocity.

When Objects Stick Together

When two objects stick together in a collision, we apply momentum conservation with a key insight:

• Before: Two separate objects with their own velocities
• After: One combined object with a single velocity

Mathematical approach:

\[m_1 v_1 + m_2 v_2 = (m_1 + m_2)v_{final}\]

Notice that the final mass is the sum of both original masses, since they’re now moving together as one unit.

Worked Example: Perfectly Inelastic Collision

A 1500 kg car traveling at 20 m/s collides with a 1000 kg stationary car. The cars stick together after collision. Find their final velocity.

Given:

• Car 1: $m_1 = 1500$ kg, $v_1 = 20$ m/s
• Car 2: $m_2 = 1000$ kg, $v_2 = 0$ m/s
• After collision: combined mass $(m_1 + m_2) = 2500$ kg

Solution:

\[m_1 v_1 + m_2 v_2 = (m_1 + m_2)v_{final}\] \[(1500)(20) + (1000)(0) = (2500)v_{final}\] \[30,000 kg \cdot m/s + 0 = 2500\,\text kg \cdot v_{final}\] \[v_{final} = 12 \text{ m/s}\]

Physical Interpretation:

• The moving car had momentum of 30,000 kg⋅m/s
• After sticking together, this momentum is shared between both cars
• The larger combined mass (2500 kg) results in a slower final velocity (12 m/s)
• Total momentum is conserved: 30,000 kg⋅m/s before = 30,000 kg⋅m/s after

Key Differences Between Collision Types

Collision Type	Objects After Impact	Final Velocities	Example
Elastic	Separate objects	Different velocities	Billiard balls bouncing
Perfectly Inelastic	Combined object	Same velocity	Cars in a crash sticking together

---

Part V: Applying Momentum Conservation

Real-World Predictions

Using our momentum equations, we can predict outcomes in real collisions, such as:

• Vehicle crashes and safety design
• Sports impacts (football tackles, baseball collisions)
• Spacecraft docking procedures
• Any collision between two objects

Problem-Solving Steps

1. Identify the masses and initial velocities of both objects
2. Apply conservation of momentum: $p_{before} = p’_{after}$
3. Solve for the unknown quantity using algebra
4. Check if the answer makes physical sense

Example Problem

A 6000 kg truck traveling at 30 m/s rear-ends a 1000 kg car traveling at 3 m/s.

Given:

• Truck: $m_A = 6000$ kg, $v_A = 30$ m/s
• Car: $m_B = 1000$ kg, $v_B = 3$ m/s
• After collision: truck velocity $v_A’ = 23$ m/s

Find: Car’s final velocity ($v_B’$)

Solution:

\[m_A v_A + m_B v_B = m_A v_A' + m_B v_B'\] \[(6000)(30) + (1000)(3) = (6000)(23) + (1000)v_B'\] \[180,000 + 3,000 = 138,000 + 1000v_B'\] \[183,000 = 138,000 + 1000v_B'\] \[v_B' = 45 \text{ m/s}\]

---

Looking Ahead

Our discovery of momentum conservation raises new questions:

• How does the force applied during a collision relate to momentum change?
• How does the time duration of the collision affect the outcome?
• Can we predict the forces involved if we know the momentum changes?

These questions will guide our next investigation into the relationship between force, time, and momentum change - leading us to discover the impulse-momentum theorem.